A pesquisa binária resolve um problema de busca e é um dos primeiros algoritmos que temos contato ao estudar programação. Logo, neste artigo abordarei de forma simples o funcionamento e aplicação em código desse algoritmo.

Introdução

O funcionamento da pesquisa binária consiste em encontrar um elemento intermediário e eliminar metade dos elementos restantes a cada vez. Vamos entender isso a seguir.

Imagine que você está procurando uma palavra no dicionário que começa com a letra O. Você abre a primeira página e vai folheando até chegar aos Os ou começa pela metade porque sabe que Os estão mais próximos?

Bem, faz mais sentido você começar pela metade, pois se você começar na primeira página e ir folheando até chegar na palavra desejada vai levar muito mais tempo. Como resultado mais tempo de processamento. Essa é a ideia da pesquisa binária.

O que a pesquisa binária faz é encontrar o elemento que estamos buscando, caso ele exista, e devolver a sua localização. A compreensão fica melhor se considerarmos uma lista ordenada. A pesquisa binária retorna a localização de um elemento dessa lista com o menor número de etapas possíveis.

Exemplo

Imagine uma lista com cem números e desejamos retornar a posição do número 57. A pior maneira de devolver a localização deste número na lista é ir eliminando número por número até chegar ao 57. É equivalente a abrir a primeira página do dicionário e ir folheando até chegar aos Os. Portanto é mais custoso.

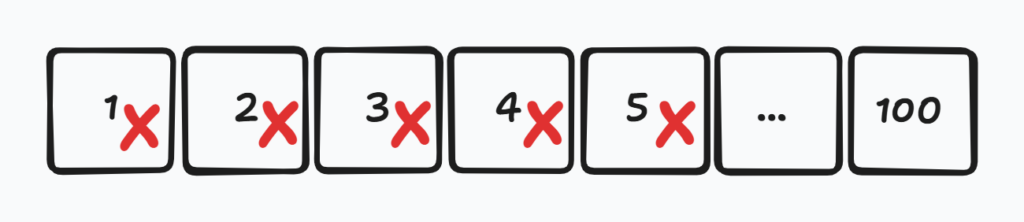
Esse método de busca é conhecido como pesquisa simples. A cada etapa eliminamos apenas um número. Pense se o número desejado fosse o 100. Precisaremos de 99 etapas para chegar até ele.

Com a pesquisa binária temos uma técnica melhor de busca. Considere a mesma lista, mas agora começamos com um número intermediário, ou seja, o número do meio. Nessa lista será o número 50.

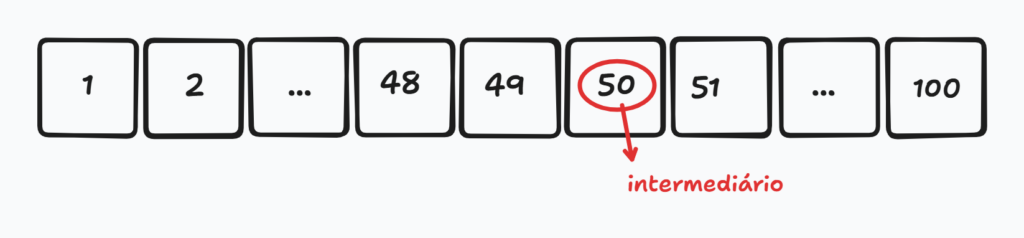
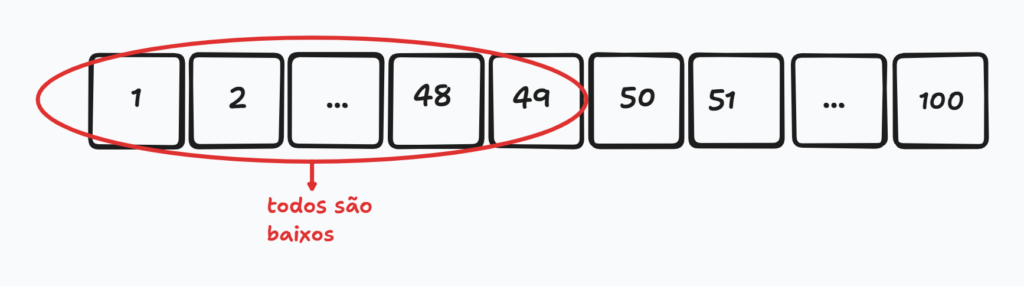
Chutamos um número baixo, pois estamos procurando o 57, mas isso foi o suficiente para eliminar metade dos números. Sabemos que os números de 1 a 50 são muito baixos. Logo podemos descartá-los.

Em seguida chutamos mais um número intermediário (entre 50 e 100). Será o 75. Levando em conta o que procuramos, é um número muito alto, mas novamente eliminamos metade dos números restantes.

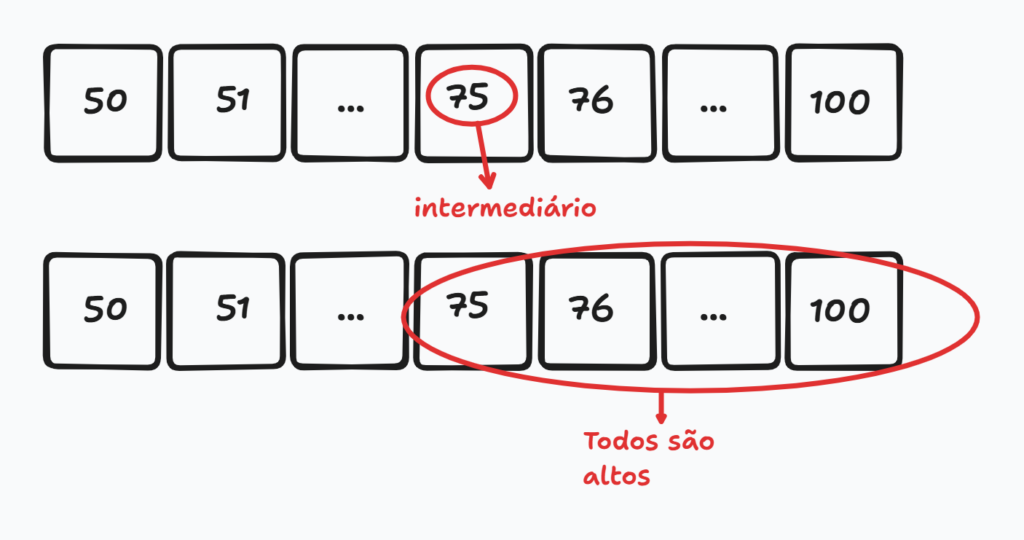
O próximo número é o 62 (entre 50 e 75). Observe que já estamos próximo do número que buscamos. Fazemos essas etapas (chuta um número intermediário e elimina metade) até encontrarmos o número que desejamos. Essa é a pesquisa binária na sua essência.

Exemplo prático

Vejamos agora a aplicação desse algoritmo em código. Usei a linguagem de programação Go para o exemplo. Caso queira aprender mais sobre essa linguagem acompanhe nossa trilha back-end Go.

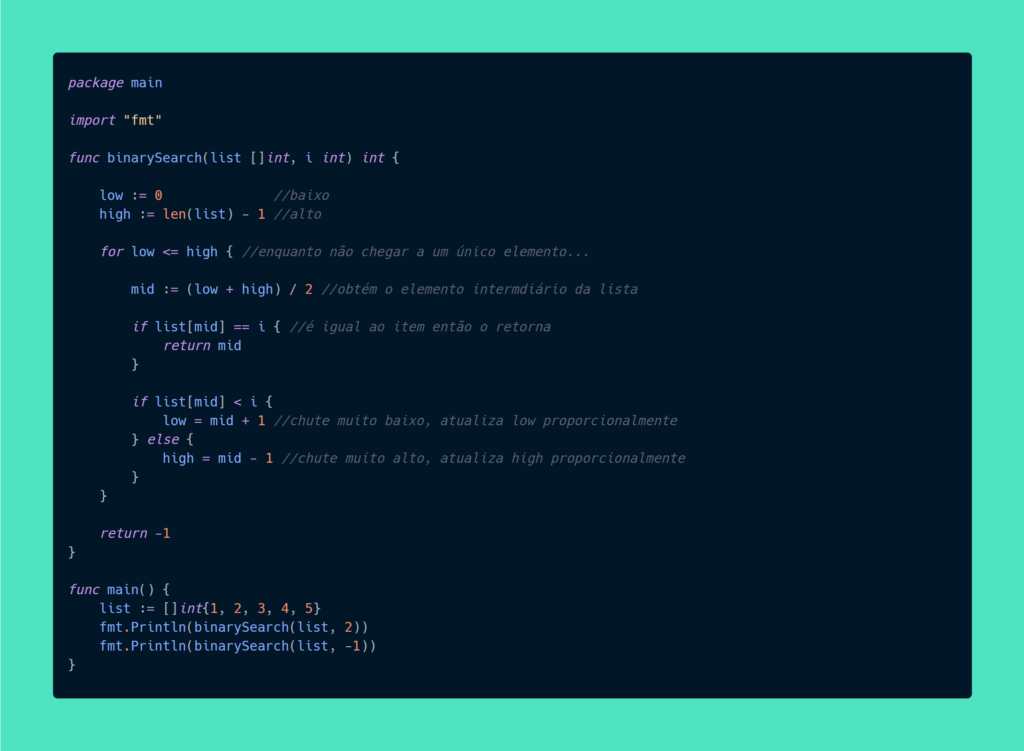
Ponto importante a destacar é que a pesquisa binária só funciona quando a lista está ordenada. No dicionário as palavras estão em ordem alfabética, imagine procurá-las se não estivessem? A pesquisa binária não se aplicaria.

Vamos entender passo a passo esse código.

• A função binarySearch pega um array ordenado e um item
• As variáveis low (baixo) e high (alto) são respectivamente o primeiro e último elemento da lista e eles acompanham a parte da lista que estamos procurando

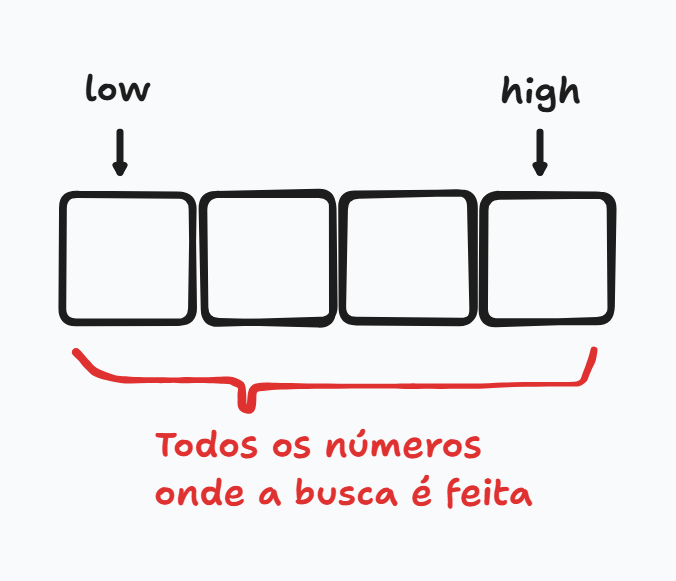
• Enquanto ainda não conseguimos chegar a um único elemento, por isso usamos o laço for nesse formato, semelhante ao while em outras linguagens de programação
• A cada tentativa testamos para o elemento central pela variável mid (meio). Arredondamos para baixo caso o número não seja par e pegamos esse número intermediário da lista
• Verificamos se o elemento central corresponde ao item procurado, caso verdadeiro retornamos esse item
• Se o chute for muito alto, atualizamos a variável alto proporcionalmente
• Se o chute for muito baixo, atualizamos a variável baixo proporcionalmente
• Se retornar -1 é porque o item não existe
• Testamos a função com a lista ordenada list

Conclusão

Com a pesquisa binária eliminamos muitas possibilidades, pois a cada etapa dela eliminamos o número de elementos pela metade até que só reste um elemento.

Em uma lista de 8 itens, por exemplo, precisamos de no máximo 4 etapas na pior das hipóteses para retornar o valor correto já que estamos sempre eliminando a metade a cada etapa.

O tempo de execução da pesquisa binária é logarítmico. Mas como assim tempo de execução logarítmico? Esse assunto será abordado com mais detalhes em outro artigo  sobre Notação Big O. Até mais!